Hydrodynamic turbulence: Turbulence is at the backbone of the research conducted in FLiP. Our group has done a large number of massive direct numerical simulations (DNS) of homogeneous and isotropic turbulence, to study intermittency, mixing, turbulent diffusion, and transport. Some of the simulations were performed using over 100,000 processors in different supercomputers, using codes developed by our group, such as GHOST (freely available on GitHub), and other codes developed by Pablo Dmitruk and Pablo Mininni. We collaborate in the development of visualization software for massive simulations of turbulence. Also, our group has studied and implemented subgrid and regularization models for the Navier-Stokes equation and for isotropic and homogeneous turbulence.
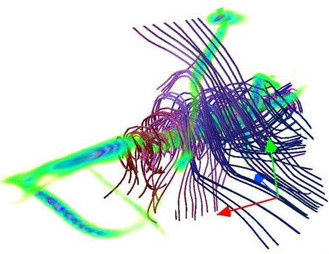
Particle dispersion: We study particle dispersion in laboratory experiments and in numerical simulations of hydrodynamic turbulence, with special interest in the development of stochastic models for single-particle dispersion in isotropic and homogeneous turbulence, as well as in atmospheric flows. Studies of particles transported by turbulent flows include the development of particle tracking techniques in the laboratory, of instrumented particles, of floaters in free surface flows, as well as of visualization methods for numerical and experimental data. Applications include the study of particles in volcanic clouds, and particle clustering in unsteady turbulence.
von Kármán flows: We study particle-laden von Kármán flows in laboratory experiments, and compare their properties with direct numerical simulations of Taylor-Green flows, to build a comprehensive database of particle dynamics in turbulence. Experimental measurement methods include particle image velocimetry (PIV) and particle tracking velocimetry (PTV), while numerical modeling of particles is done using GHOST. For videos of the experiments, visit our YouTube channel.

Surface wave turbulence: We study surface wave turbulence in laboratory experiments, and characterize wave turbulence regimes using techniques developed specifically for this problem by Pablo Cobelli and collaborators, such as Fourier transform profilometry, as well as other techniques as, e.g., particle image velocimetry and particle tracking velocimetry. These techniques allow us to measure the spatio-temporal spectrum, as well as other properties of the linear and non-linear waves in the flow. Recently we established a relation between surface wave turbulence and critical phenomena through conformal invariance.

Two dimensional flows: Two dimensional flows display an inverse cascade of energy: energy is transferred from small to large scales, resulting in the growth of large-scale structures and in a self-organization process. Although a simplification of more complex flows, two dimensional turbulence provides insight into the dynamics of atmospheric, oceanic, and space physics flows. Our group has studied the decay of enstrophy in two-dimensional flows, inverse cascades in these flows, and turbulence in quasi-geostrophic flows.

Rotating flows: Rotation plays a central role at the largest-scales of geophysical and planetary flows. Flows in a rotating frame transfer energy preferentially towards two-dimensional modes, developing strong anisotropy and column-like structures. Among other studies, our group is interested in the effect of rotation in helical and non-helical flows, the recovery of isotropy at small scales in a simulation or rotating turbulence at very large Reynolds number using 30723 grid points, and quantified the relevance of inertial waves in rotating turbulence.

Stratified flows: Planetary and the Earth’s atmosphere display layers and stratification, as a result of the effect of gravity and buoyancy forces acting in the flow. Stratification results in the development of pancake-like structures and of vertically-sheared horizontal winds. At intermediate scales in the atmosphere and the oceans, the interplay between rotation and stratification also results in slanted layers in the velocity and the temperature fields. To see what our group does in this field, you can read a study on intermittency and extreme events in stratified turbulence , or the results of a massive simulation of rotating and stratified turbulence using 40963 grid points. Recently we published in Science Magazine a study of inverse cascades in rotating and stratified flows with realistic atmospheric parameters.

Wall bounded turbulence: FLiP! develops and maintains several codes to study turbulence in periodic boundary conditions (as GHOST), as well as other codes to study wall bounded turbulence. All codes are parallelized and scale well in state of the art supercomputers. SPECTER is a pseudospectral code to study channel flow and Rayleigh-Bénard convection, using a novel Fourier-continuation technique. SPHERE is another code to study neutral and conducting flows inside spheres, using a purely spectral method with Chandrasekhar-Kendall basis. All codes are publicly available, and work with VAPOR for 3D visualization.

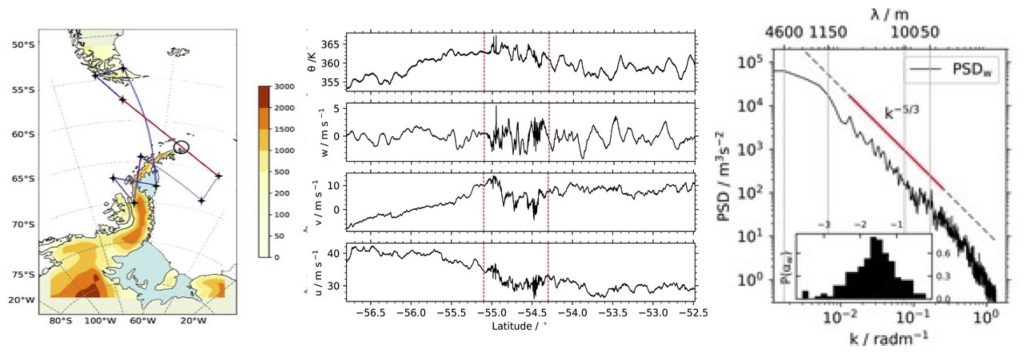
Atmospheric turbulence: Clear air turbulence is a phenomenon that occurs in the upper troposphere and lower stratosphere (between 8 and 15 km, where most commercial flights take place), and which is not associated with clouds or thunderstorms. This unexpected and difficult-to-predict phenomenon is hazardous for aviation, as is neither visible to pilots nor detectable by standard on-board radars. We use high-resolution in situ aircraft measurements to study turbulent coefficients such as the turbulent kinetic energy and the dissipation rate, as a way to improve our understanding of atmospheric turbulence. Different techniques to study and characterize anisotropic turbulent transport and mixing at flight level due to stable stratification and rotation also include the use of spectral methods, structure functions, and the visualization of the large scale atmospheric scenario using numerical weather forecast models.
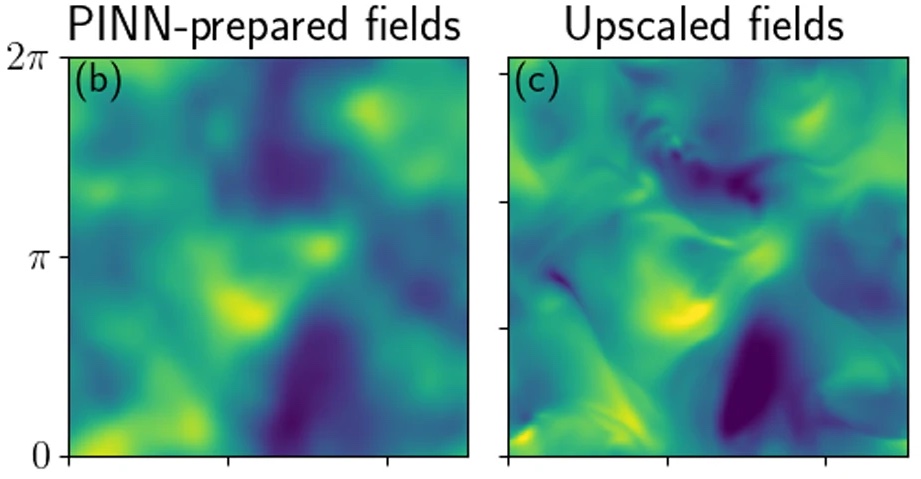
Physics informed neural networks: Patricio Clark di Leoni and other group members use machine learning and data science methods to study turbulence, Rayleigh-Bernard convection, particle laden flows, and to develop data assimilation methods for fluid dynamics from experimental data, with a special emphasis on applications of physics informed neural networks on these topics.